This is an experiment to publish both an article and a Twitter thread. The individual tweets are numbered and linked after each paragraph/section.
A recent misleading article
I believe this article on false positives with PCR tests is misleading. It seems to only apply simple math to a problem with some wrong assumptions. It baffles me, as Carl Heneghan is a medical professor and I'm not, yet I spot some obvious errors. 😕 🐦1
Specificity & Sensitivity with multi-target tests
Most important of all, what seems to be lacking in the article is the huge difference in specificity when it comes to the number of targets testing for. PCR aims for finding a certain sequence in the genetic material (gene, the target). 🐦2
If we would be testing for a single target, this would result in quite a lot false positives—in the order of magnitude ~ 1-3 per cent. Reasons include a gene that's not specific to SARS-CoV-2 or a tiny viral fragment that somehow ended up in the sample as noise/contamination. 🐦3
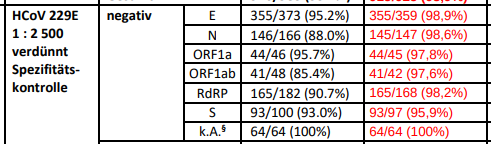
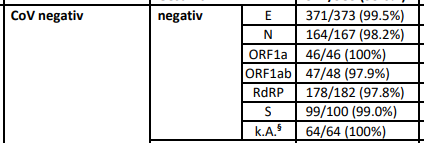
A German test report on PCR tests shows the characteristics on different genes/targets. It was used by Dutch skeptics as proof that PCR tests are unreliable, but in fact it shows a completely different result. Some picks shown on the right. 🐦4
A single sample run with multiple targets is basically running separate tests. More than one 'test error' to occur is mathematically very unlikely to happen as well as a false positive to an error in specificity.
Running with multiple targets leads to a much lower false positive rate at the expense of an increased false negative rate. 🐦5
This should lead to a much lower false positive rate at the expense of an increased false negative rate. 🐦6
Here's an example calculation with testing for both E and N gene. Assuming respectively 99.5% and 98.2% correctness on a known-negative sample (from that German paper). This means 0.5% multiplied by 1.8% = 0.009% chance that both genes show (false) positive. 🐦7

Of course, single-target testing is probably cheaper and faster, but should never happen in low-prevalence areas for the reasons described in the Spectator article. This is just part of the guidance/procedures in testing! WHO guidance document from March. 🐦8
PCR test results aren't binary
Also please don't mistake PCR testing for a test with a binary outcome. The testing machines produce a response curve over time of amplification. Sometimes these curves aren't proving a very clear outcome and a human should interpret the raw results. 🐦9
In case of doubt, they may supply additional notes with the diagnostics outcome. This really happens. For example, this case in The Netherlands. A sample of people at a meat factory mostly indicated curves that fit the "found a case too late" picture. BD: Steekproef Vion in Boxtel 🐦10
That nuance can be part of the test result! With this notes on the results, the persons were informed that they are likely not infectious any longer. I think that's a great result and not to be considered a false positive. 🐦11
It also demonstrates that if the curves are showing inconclusive, the test result can come back as inconclusive as well. Perhaps you will be asked to test again. 🐦12
Reality in mass testing
Now, here's a well-documented example that proves the point from the reality. 11 million people were mass-tested in China. How many positives? 206. Even if zero were infected, it's only 0,00187% false positive and professor Heneghan is off by about factor 50. 🐦13
Then, finally, it's typically not a random group of people being tested, so the factor of 50 is likely even bigger. Valid point by @regordane. 🐦14
Summary
To summarize: I think given these examples, the article by Carl is misleading. In practice health authorities and labs are perfectly aware of the shortcomings of PCR and act accordingly to avoid the pitfall he's describing. 🤷 🐦15
Applying just math to a binary problem that's not binary to begin with, ignoring multi-target testing in the probability calculation, is plain wrong in my opinion. 🐦16
Comments on this blog post are disabled; please use Twitter to reply with your comments—thanks.